4.1 Amostragem e Quantização

A Figura 4.1 mostra uma imagem sintética, gerada a partir do computador. Esta imagem está sendo gerada a partir de informações de uma arte vetorial, e portante está sendo adquirida e processada de maneira digital.

Figura 4.1: Imagem sintética, gerada de maneira digital por um computador a partir de uma imagem em representação vetorial.

Caso essa imagem fosse capturada a partir de um sinal analógico, iriamos obter algo mais semelhante com a Figura 4.2 onde a imagem contêm pequenas imperfeições que são resultantes do ruído do sinal, note que está imagem continua representa um sinal capturado em uma escala de cinzas.

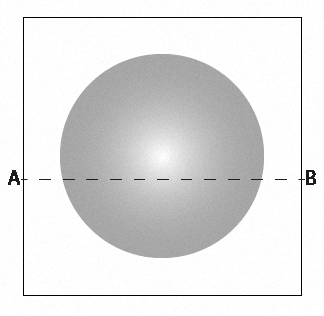
Figura 4.2: Representação de uma imagem contínua em escala de cinzas.

A Figura 4.2 ilustra uma imagem contínua f que queremos converter em formato digital. Uma imagem contínua é uma imagem que ainda não foi digitalizada.

Uma imagem pode ser contínua em relação às coordenadas $x$ e $y,$ e também em amplitude. Para digitalizá-la, temos que amostrar a função em tanto em suas coordenadas $(x,y)$, como também em sua amplitude.

A digitalização dos valores das coordenadas é chamada de amostragem. Já a digitalização dos valores de amplitude é chamada de quantização.

Amostragem

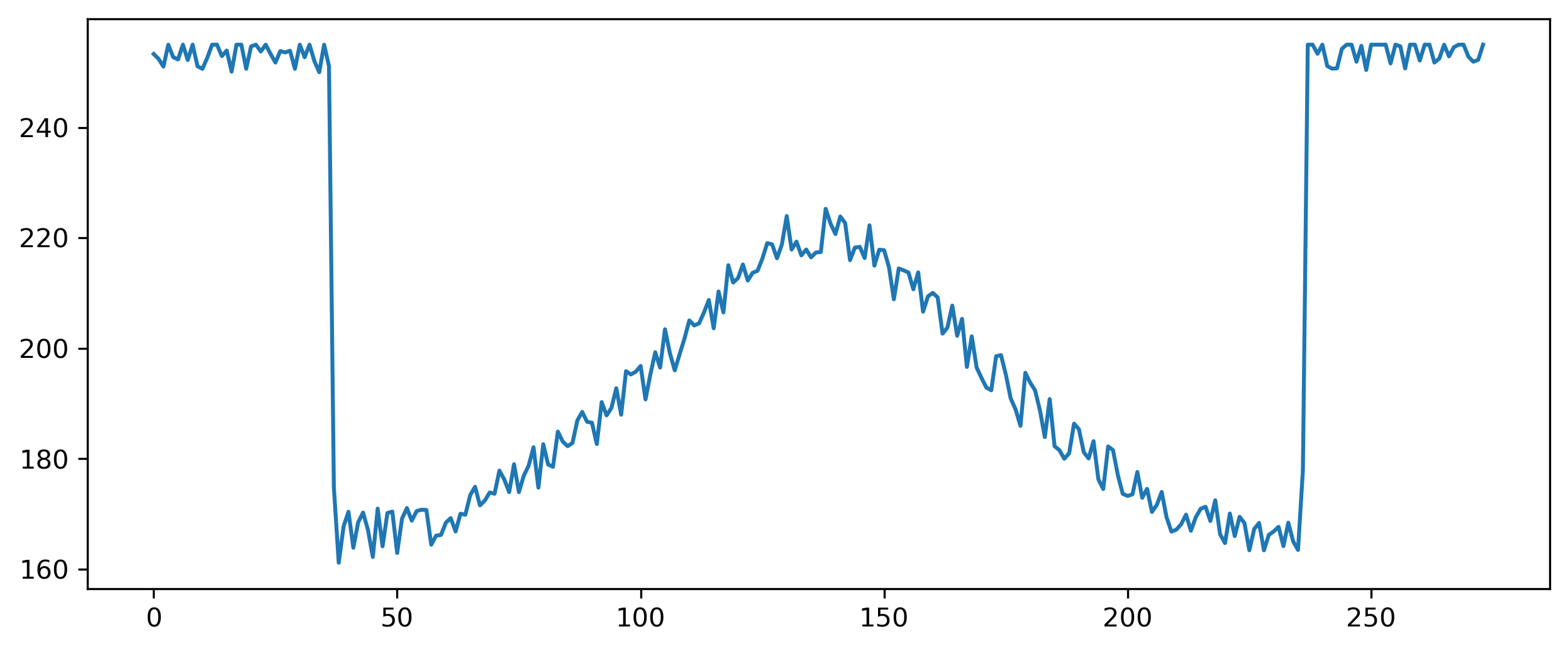
Figura 4.3: Níveis de intensidade de uma imagem contínua em escala de cinzas.

A função unidimensional na Figura 4.3 é um gráfico dos valores de amplitude (nível de intensidade) da imagem contínua exibida anteriormente. Estas intensidades foram obtidas ao longo do segmento de linha $AB$ desta mesma Figura 4.2. As variações aleatórias são devido ao ruído da imagem.

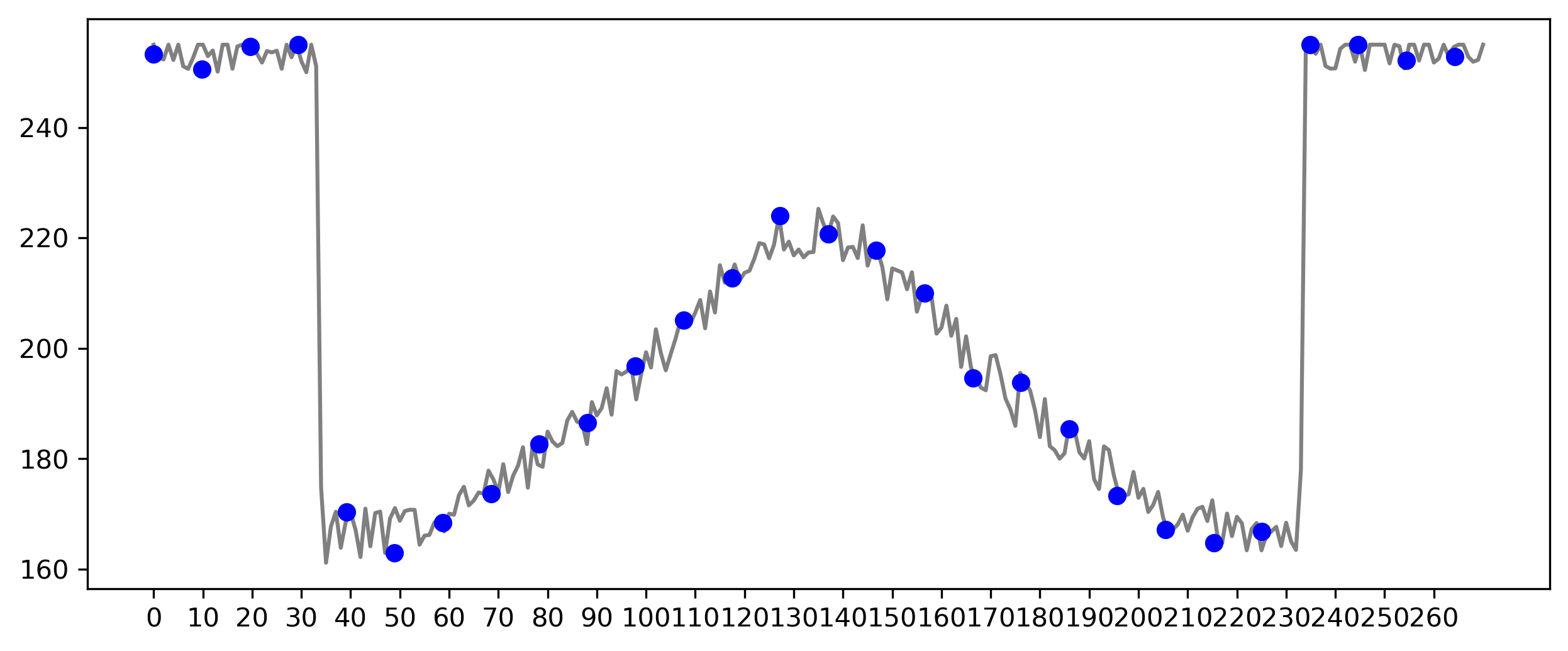
Figura 4.4: Níveis de intensidade de uma imagem amostrada em intervalos discretos.

Para realizar a amostragem desta função, tomamos amostras igualmente espaçadas ao longo da linha $AB$, como mostrado na 4.4. As amostras são ilustradas na figura como os pontos azuis escuros sobrepostos à função, e suas localizações espaciais (discretas) são indicadas pelas marcas correspondentes na parte inferior da figura. O conjunto que contêm todos os pontos azuis escuros constitui a função amostrada. No entanto, os valores das amostras ainda abrangem (verticalmente) uma faixa contínua de valores de intensidade.

Exercício 1 - Amostragem

Utilizando os conceitos vistos nesta seção, faça a re-amostragem de uma imagem:

Escolha uma imagem com uma boa resolução espacial. Utilizando apenas operações matemáticas básicas e manipulação de np.array faça uma re-amostragem da imagem, diminuindo a resolução espacial da imagem resultante. Utilize um parâmetro para controlar qual o intervalo de amostragem espacial utilizado.

Um exemplo do resultado desejado pode ser visto abaixo:

Figura 4.5: Imagem Original

• Utilize uma imagem inicial qualquer de sua escolha, com dimensões adequadas.
• Utilize apenas funções do numpy para realizar a re-amostragem.
• Não utilize a função cv.resize para realizar a amostragem, porém, você pode utilizar essa função para salvar a imagem em uma resolução espacial maior. Isso é necessário, pois ao re-amostrar a imagem, a imagem resultante pode ter resolução espacial menor

Quantização

Para formar uma função digital, os valores de intensidade também devem ser convertidos (quantizados) em quantidades discretas.

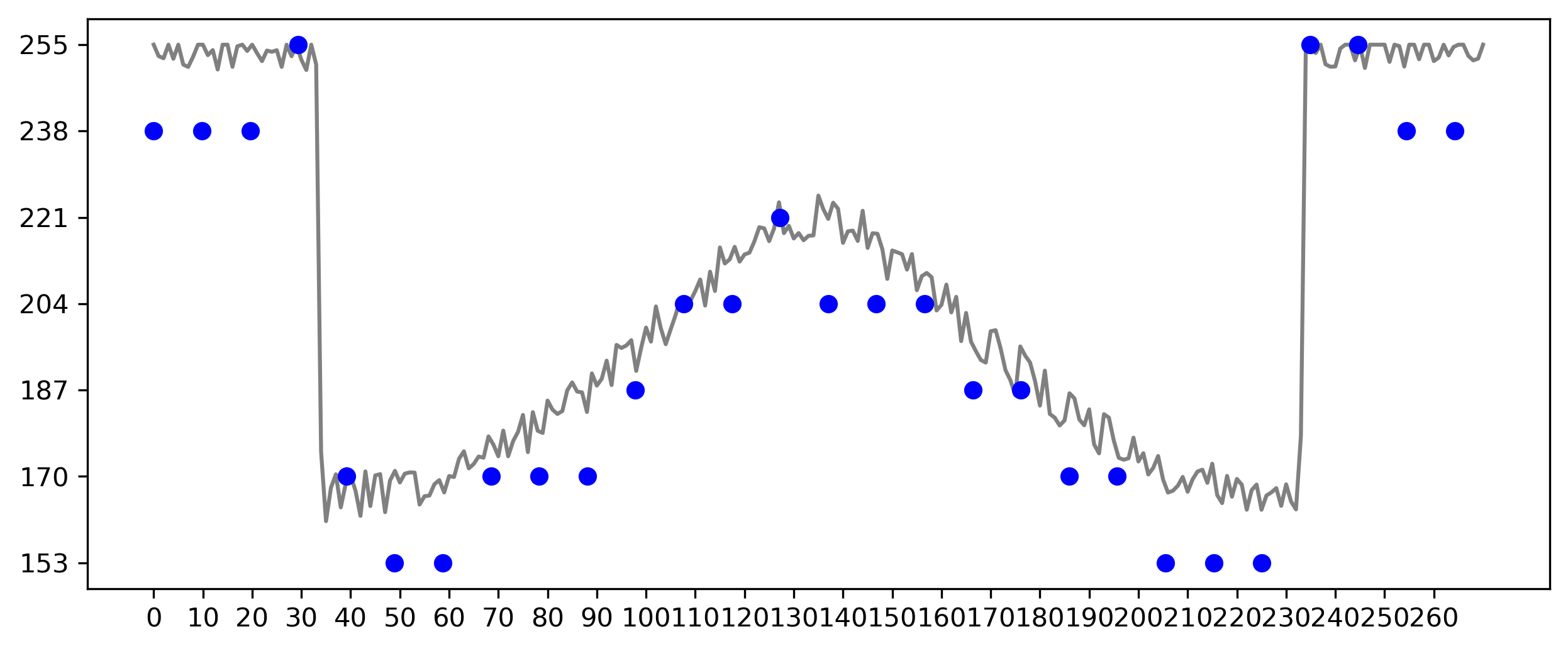
Figura 4.6: Níveis de intensidade quantizados em 8 níveis em uma imagem amostrada em intervalos discretos.

A Figura 4.6 mostra um gráfico com o sinal original, e sua escala de intensidade dividida em $8$ intervalos discretos, variando de preto a branco. As marcas verticais indicam o valor específico atribuído aos intervalos de intensidade com valor superior a $150$ (valor determinado pela intensidade mínima do sinal de entrada). Os níveis de intensidade contínua são quantizados atribuindo um dos oito valores a cada amostra, dependendo da proximidade vertical de uma amostra a uma marca vertical. Como o sinal original não possui intensidades com valor próximos a $0$, em uma escala de $0$ a $255$, um intervalo dessa quantização não esta sendo utilizados nesta imagem.

As amostras digitais resultantes tanto da amostragem quanto da quantização são mostradas como bolinhas azuis na Figura 4.6. Note que essa configuração de quantização e amostragem gera uma reconstrução bastante rudimentar do sinal original.

Começando no topo da imagem contínua e realizando este procedimento para baixo, linha a linha, produz-se uma imagem digital bidimensional. Levando em consideração a quantização acima, a imagem original teria o seguinte aspecto:

Figura 4.7: Imagem quantizada em 8 níveis de cor

Analisando as Figuras 4.6 e 4.7, podemos perceber que além do número de níveis discretos usados, a precisão alcançada na quantização é altamente dependente do conteúdo de ruído do sinal amostrado. Na prática, o método de amostragem é determinado pelo arranjo do sensor usado para gerar a imagem.

Quando uma imagem é gerada por um sensor de único elemento, combinado com movimento mecânico, como na Figura 4.8, a saída do sensor é quantizada da maneira descrita acima. No entanto, a amostragem espacial é realizada selecionando o número de incrementos mecânicos individuais nos quais ativamos o sensor para coletar dados. O movimento mecânico pode ser muito exato, então, em princípio, o limite para o quão fino podemos amostrar uma imagem usando essa abordagem não é a limitação primordial da técnica de amostragem. Na prática, os limites de precisão da amostragem são determinados por outros fatores, como a qualidade dos componentes ópticos usados ​​no sistema.

Figura 4.8: Dispositivo (sensor) mecânico de um único elemento

Quando uma faixa de detecção é usada para aquisição de imagem (muito comum em dispositivos como scanners de mesa), o número de sensores na faixa estabelece as amostras na imagem resultante em uma direção e o movimento mecânico estabelece o número de amostras na outra. A quantização das saídas do sensor completa o processo de geração de uma imagem digital.

Quando uma matriz de detecção é usada para aquisição de imagem (como nas câmeras digitais), nenhum movimento é necessário. O número de sensores na matriz é fator que estabelece os limites de amostragem em ambas as direções. A Figura 4.9 ilustra esse conceito.

Figura 4.9: Imagem obtida por sensor do tipo matriz de detecção com uma matriz de tamanho 16 x 16

Podemos projetar a Figura 4.1, que é uma imagem contínua. no plano de um sensor $2D$. A Figura 4.9 mostra a imagem após amostragem e quantização. Como podemos perceber, a qualidade de uma imagem digital é determinada em grande parte pelo número de amostras e níveis discretos de intensidade usados ​​na amostragem e quantização. No entanto, como mostraremos nos próximos capítulos que o conteúdo da imagem também desempenha um papel na escolha desses parâmetros.

Exercício 2 - Quantização

Utilizando os conceitos vistos nesta seção, faça a quantização de uma imagem em níveis menores que a imagem original:

Escolha uma imagem com uma quantização de cores suficiente, preferencialmente com 256 intensidades para cada canal de cor.

Utilizando apenas operações matemáticas básicas e manipulação de np.array faça a quantização, diminuindo os níveis de intensidade a cada etapa. Utilize um parâmetro para controlar o nível de quantização de intensidades desejados.

Um exemplo do resultado desejado pode ser visto abaixo:

Figura 4.10: Imagem Original

• Utilize uma imagem inicial qualquer de sua escolha, com dimensões adequadas.
• Utilize apenas funções do numpy para realizar a re-amostragem.
• Não utilize a função cv.resize para realizar a amostragem, porém, você pode utilizar essa função para salvar a imagem em uma resolução espacial maior. Isso é necessário, pois ao re-amostrar a imagem, a imagem resultante pode ter resolução espacial menor