5.1 Interpolação

A interpolação é uma operação matemática que, entre outras finalidades, permite obter o valor de uma função em um eixo qualquer a partir de uma sequência de amostras. A técnica mais trivial, chamada de vizinhos mais próximos, consiste em escolher a amostra mais próxima da posição desejada e tomar o seu valor como valor desta posição. Está técnica é muito utilizada para exibir imagens em uma resolução espacial maior que as suas amostras. Utilizamos essa técnica nos exercícios do Capítulo 4 .

Em Python, a função resize do OpenCV realiza essa operação na função resize através do parâmetro interpolation com o valor INTER_NEAREST :

image = io.imread("...imagem.png")

interpolated = cv.resize(sa_img, (image.shape[1], image.shape[0]), 
                         interpolation = cv.INTER_NEAREST)
plt.imshow(interpolated)

Essa forma de gerar imagens é particularmente interessante quando se trata em preservar os detalhes de imagens com baixa resolução espacial. Esta técnica é muito utilizada para gerar imagens de jogos antigos em dispositivos de exibição modernos.

O exemplo abaixo é do jogo Super Mario World do vídeo-game Super Nintendo:

Na imagem superior, temos uma cena do jogo Super Mario World em sua resolução original $254\times 224$, e logo abaixo, a mesma cena utilizando um algoritmo de vizinhos mais próximos para a resolução de $1280\times 1120$. Nesse tipo de operação, é possível preservar totalmente a informação caso o fator de escala seja um inteiro, no exemplo dessa imagem, aumentamos a resolução em um fator $5$ da resolução original.

Exercício

Tente reproduzir o resultado acima, porém utilizando apenas operações do numpy. Considerando que cada bloco de tamanho $5\times 5$ pixels da nova imagem irá corresponder a um único pixel da imagem original.

Como exemplo, no primeiro bloco de pixel da nova imagem, podemos copiar um único pixel da posição $(0,0)$ da imagem original utilizando:

imagem[0:5, 0:5, :] = mario1[0, 0, :]

Outra técnica muito utilizada é a interpolação linear e a interpolação bilinear. Nela um determinado ponto na nova imagem é gerado a partir a interpolação de pontos mais próximos, para um sinal unidimensional, isso significa gerar novos valores aproximados a partir de amostras próximas.

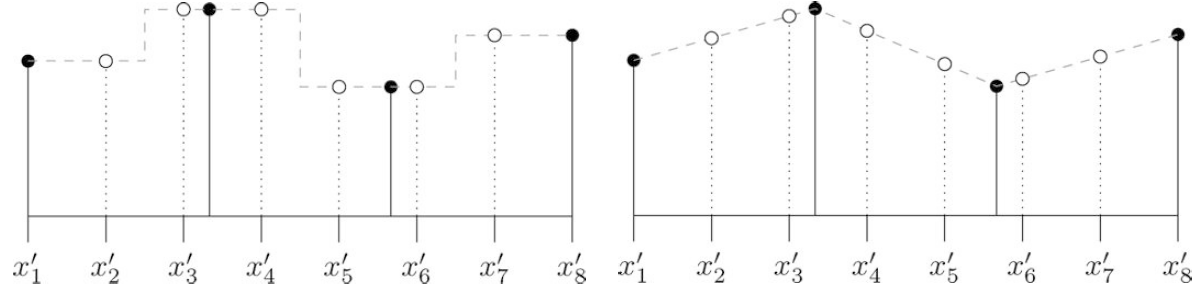
Figura 5.1: Sinal $1D$. Os pontos preenchidos são amostras do sinal. Novos pontos gerados utilizando algoritmo de vizinhos mais próximos (esquerda) e de interpolação linear (direita)

Na imagem acima é possível perceber que o algoritmo de interpolação linear produz novos valores, produzindo uma representação de um sinal mais suave.

O calculo de um novo ponto $F$ utilizando interpolação a interpolação linear entre os pontos $x_1$ e $x_2$ é dada por:
$$\begin{array}{cc}F& =\lambda f\left(x_2\right)+(\lambda -1)f\left(x_1\right)\end{array}$$

onde $\lambda$ é um parâmetro que define a distância linear do ponto F a partir do ponto $x_1$ até o ponto $x_2$.

Para imagens, podemos aplicar os mesmos princípios, porém com um domínio em duas dimensões. Esse tipo e interpolação faz uso da interpolação linear para gerar um ponto em duas dimensões, ele é chamado de interpolação bilinear.

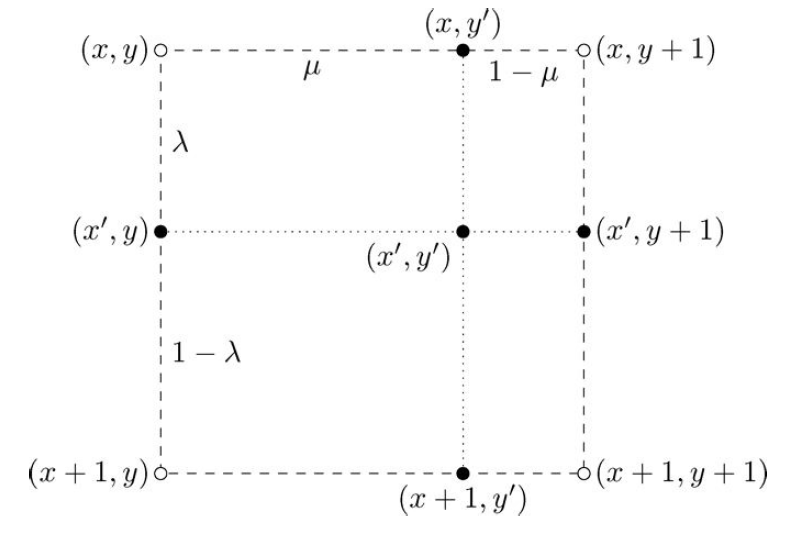
Figura 5.2: Interpolação bilinear. Os pontos preenchidos são amostras do sinal. O novo ponto $(x^{\prime },y^{\prime })$ é gerado utilizando interpolação bilinear.

Para gerar o ponto $(x´,y´)$ da figura 5.2, utilizamos os seguintes passos:

1. Primeiro calculamos o ponto $(x,y^{\prime })$ a partir da interpolação linear dos pontos $(x,y)$ e $(x,y+1)$
2. Em seguida, calculamos o ponto $(x+1,y^{\prime })$ a partir da interpolação linear dos pontos $(x+1,y)$ e $(x+1,y+1)$
3. Finalmente, calculamos o ponto $(x´,y´)$ a partir da interpolação dos dois pontos calculados anteriormente.

Matematicamente, essas operações são equivalentes a: $$\begin{array}{cc}f(x,y^{\prime })& =\mu f(x,y+1)+(\mu -1)f(x,y),\\ f(x+1,y^{\prime })& =\mu f(x+1,y+1)+(\mu -1)f(x+1,y),\\ f(x,y^{\prime })& =\lambda f(x+1,y^{\prime })+(\lambda -1)f(x,y^{\prime }),\end{array}$$

substituindo as duas primeiras equações na terceira, temos a formula da interpolação bilinear:

$$\begin{array}{cc}f(x,y^{\prime })& =\lambda \mu f(x+1,y+1)+(\mu -1)f(x+1,y)\\ & +(\lambda -1)\mu f(x,y+1)+(\mu -1)f(x,y).\end{array}$$

O OpenCV também implementa essa operação na função resize ao especificar o valor INTER_LINEAR ao parâmetro de interpolação:

image = io.imread("...imagem.png")

interpolated = cv.resize(sa_img, (image.shape[1], image.shape[0]), 
                         interpolation = cv.INTER_LINEAR)
plt.imshow(interpolated)

A imagem acima exibe a mesma figura utilizada anteriormente como exemplo, porém reconstruída utilizando a interpolação bilinear. Note como a imagem ficou com aparência suavizada, principalmente em relação as bordas. Esse efeito pode ser benéfico para imagens naturais, porém pode não ser desejado, como é o caso desse exemplo, onde normalmente é preferível manter o aspecto de pixel art da imagem original.

Exercício

Implemente uma função que faz a interpolação bilinear entre 4 pontos arbitrários utilizando apenas operações do numpy.

Existem diversas formas diferentes de realizar operações de interpolação, para imagens, estão a interpolação bi-cúbica e o algoritmo de Lanczos. Ambos estão disponíveis no OpenCV, embora mais custosos computacionalmente, esses algoritmos apresentam uma melhora na qualidade da imagem gerada.