4.2 Coordenadas

Seja $f (s, t)$ uma função que representa uma imagem contínua de duas variáveis. Convertemos essa função em uma imagem digital por amostragem e quantização, conforme explicado na seção anterior. Suponha que amostramos a imagem contínua em uma imagem digital, $f (x, y)$ , contendo $M$ linhas e $N$ colunas, onde $(x, y)$ são coordenadas discretas. Sendo assim, usaremos valores inteiros para essas coordenadas discretas, por exemplo, o valor da imagem digital na origem é $f (0, 0)$ , e seu valor nas próximas coordenadas ao longo da primeira linha é $f (0, 1)$ . Aqui, a notação $(0, 1)$ é usada para denotar a segunda amostra ao longo da primeira linha.

Em geral, o valor de uma imagem digital em qualquer coordenada $(x, y)$ é denotado por $f (x, y)$ , onde $x$ e $y$ são inteiros. A seção do plano real abrangida pelas coordenadas de uma imagem é chamada de domínio espacial, com $x$ e $y$ sendo referidos como variáveis espaciais ou coordenadas espaciais.

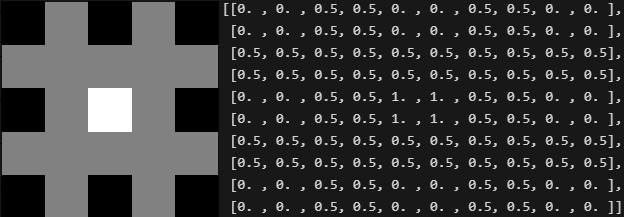
Figura 4.11: Duas representações de imagens

A Figura 4.11 mostra duas maneiras de representar $f (x, y)$ . A representação à esquerda é mais comum e exibe $f (x, y)$ como a imagem que seria exibida em uma tela de computador ou em uma fotografia. Aqui, a intensidade de cada ponto na tela é proporcional ao valor de $f$ naquele ponto. Nesta figura, existem apenas três valores de intensidade igualmente espaçados. Se a intensidade for normalizada para o intervalo $[0, 1]$ , então cada ponto na imagem tem o valor $0$ , $0.5$ ou $1.0$ . Um monitor ou impressora converte esses três valores em preto, cinza ou branco, respectivamente. Esse tipo de representação inclui imagens coloridas e nos permite visualizar os resultados rapidamente.

Como mostra à direita da Figura 4.11, essa representação utiliza uma matriz composta pelos valores numéricos de $f (x, y)$ . Esta representação foi apresentada no Capítulo 3.2. Esta é a representação mais usada para processamento de imagens em computador, onde escrevemos a imagem através de uma matriz $M \times N$ .

Utilizamos a convenção de representar a origem, como o ponto $(0, 0)$ localizado no canto superior esquerdo da imagem. O Centro da imagem é definido como o ponto $(M / 2, N / 2)$ . O exemplo abaixo cria uma imagem de tamanho $M = 4, N = 4$ e marca a origem de azul, e o centro de verde.

image = np.zeros((5,5,3), dtype=np.int32)
image[0,0,2] = 255
image[2,2,1] = 255
plt.imshow(image)
plt.show()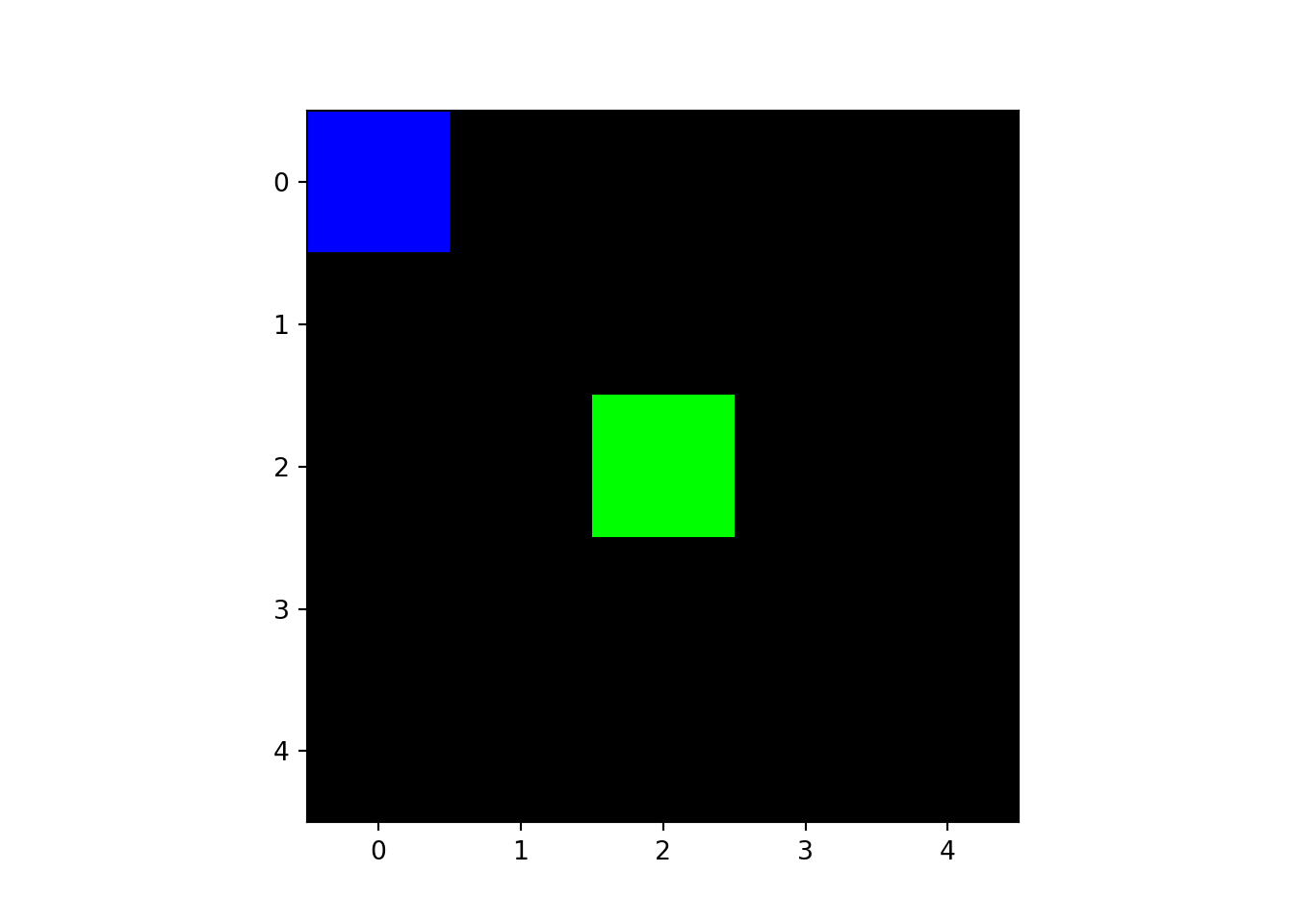

Note que usamos o terceiro índice, que indexa a cor, para definirmos a intensidade da cor em um ponto específico.

Exercício

Implemente uma imagem que simboliza uma bússola, como mostrado abaixo:

Utilize uma matriz de tamanho $5 \times 5$ para iniciar a sua imagem. Utilize as seguintes cores e combinações para chegar no resultado semelhante ao exibido acima.

norte = np.array([255, 0  , 0  ])
sul =   np.array([0  , 0  , 255])
leste = np.array([0  , 255, 0  ])
oeste = np.array([127, 127, 127])

O intervalo de valores abrangendo a escala de cinza é chamado de intervalo dinâmico, um termo usado de diferentes maneiras em diferentes campos. Aqui, definimos o intervalo dinâmica de um sistema de imagem como a razão entre a intensidade máxima mensurável e o nível mínimo de intensidade detectável no sistema.

Via de regra, o limite superior é determinado pela saturação e o limite inferior pelo ruído, embora o ruído possa estar presente também em intensidades mais leves. A saturação é o valor mais alto além do qual todos os valores de intensidade são cortados ( toda a área saturada tem um nível de intensidade alto e constante). O ruído visível aparece normalmente como um padrão de textura granulada.

A faixa dinâmica estabelece os níveis de intensidade mais baixos e mais altos que um sistema pode representar e, consequentemente, que uma imagem pode ter. Intimamente associado a este conceito está o contraste da imagem, que definimos como a diferença de intensidade entre os níveis de intensidade mais altos e mais baixos de uma imagem. A razão de contraste é a razão entre essas duas grandezas. Quando um número apreciável de pixels em uma imagem tem uma faixa dinâmica alta, podemos esperar que a imagem tenha alto contraste. Por outro lado, uma imagem com faixa dinâmica baixa normalmente tem uma aparência cinza esmaecida e desbotada.